Generalizing the Parallel Axis Theorem
Published:
Testing LaTeX on this site with some physics fun.
Generalized Parallel Axis Theorem
The (easier) Parallel Axis Theorem
To derive the parallel axis theorem, let’s consider the kinetic energy of a rotating rigid object of mass \(M\) about some axis. By definition, the kinetic energy of the object is
\[T_{sys} = \frac{1}{2} \int dm (\boldsymbol{\omega} \times \mathbf{r})^2\]where \(\mathbf{r}\) denotes the position of each infinitessimal mass element \(dm\), and \(\boldsymbol{\omega}\) is the object’s angular momentum.
Let \(\mathbf{r}_{cm}\) denote the position of the object’s center of mass and \(\mathbf{r}'\) denote the position of the mass element with respect to the center of mass. In general, I will use the prime to denote with respect to center of mass. Therefore, we can rewrite \(\mathbf{r}\) as:
\[\mathbf{r}' = \mathbf{r} - \mathbf{r}_{cm} \implies \mathbf{r} = \mathbf{r}' + \mathbf{r}_{cm}\]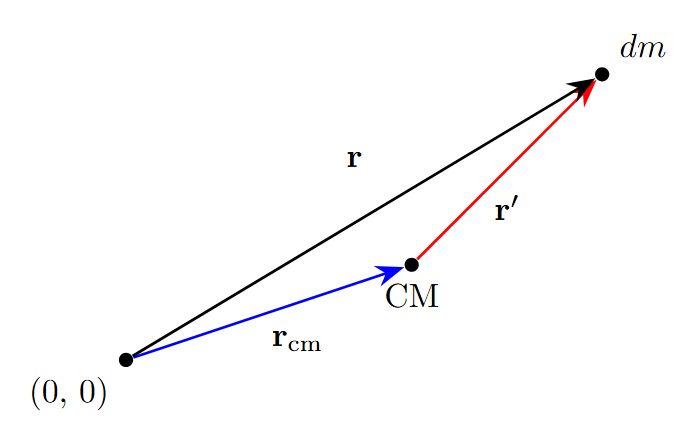
Substituting our expression for \(\mathbf{r}\) into \(T_{sys}\):
\[\begin{aligned} T_{\text{sys}} &= \frac{1}{2} \int dm \, \left[ \boldsymbol{\omega} \times (\mathbf{r}_{\text{cm}} + \mathbf{r}') \right]^2 \\ &= \frac{1}{2} \int dm \, (\boldsymbol{\omega} \times \mathbf{r}_{\text{cm}})^2 + \int dm \, (\boldsymbol{\omega} \times \mathbf{r}_{\text{cm}}) \cdot (\boldsymbol{\omega} \times \mathbf{r}') + \frac{1}{2} \int dm \, (\boldsymbol{\omega} \times \mathbf{r}')^2 \end{aligned}\]The first term reduces to \(\frac{1}{2}M v_{cm}^2\). The middle term vanishes because \(\int \mathbf{r}' \, dm = 0\). The final term is the kinetic energy in the center of mass frame, leaving:
\[\begin{aligned} T_{sys} &= \frac{1}{2}M v_{cm}^2 + T_{sys}' \\ &= \frac{1}{2}M \omega^2 r_{cm}^2 + \frac{1}{2}I' \omega^2 \\ &= \frac{1}{2}\omega^2 (M r_{cm}^2 + I') \end{aligned}\]Therefore, the moment of inertia \(I\) can be written as:
\[\boxed{ I = (M r_{cm}^2 + I') }\]which is the Parallel Axis Theorem we all know and love.
Generalizing with tensors
Let’s now replace the moment of inertia \(I\) with the inertia tensor \(\mathbf{I}\), which encodes mass distribution around all possible rotation axes.
For a rigid body rotating with angular velocity \(\boldsymbol{\omega}\), the kinetic energy is:
\[T_{\text{sys}} = \frac{1}{2} \boldsymbol{\omega} \cdot \mathbf{I} \cdot \boldsymbol{\omega}\]where the inertia tensor \(\mathbf{I}\) is defined as:
\[\mathbf{I} = \int dm \, \left[ (\mathbf{r} \cdot \mathbf{r}) \mathbf{1} - \mathbf{r} \otimes \mathbf{r} \right]\]Here, \(\mathbf{1}\) is the identity, and \(\otimes\) denotes the outer product.
Let \(\mathbf{r} = \mathbf{r}_{\text{cm}} + \mathbf{r}'\), where \(\mathbf{r}'\) is the position relative to the CM. Substituting into \(\mathbf{I}\):
\[\begin{aligned} \mathbf{I} &= \int dm \, \left[ \left( (\mathbf{r}_{\text{cm}} + \mathbf{r}') \cdot (\mathbf{r}_{\text{cm}} + \mathbf{r}') \right) \mathbf{1} - (\mathbf{r}_{\text{cm}} + \mathbf{r}') \otimes (\mathbf{r}_{\text{cm}} + \mathbf{r}') \right] \\ &= \int dm \, \left[ \left( r_{\text{cm}}^2 + 2 \mathbf{r}_{\text{cm}} \cdot \mathbf{r}' + r'^2 \right) \mathbf{1} - \left( \mathbf{r}_{\text{cm}} \otimes \mathbf{r}_{\text{cm}} + \mathbf{r}_{\text{cm}} \otimes \mathbf{r}' + \mathbf{r}' \otimes \mathbf{r}_{\text{cm}} + \mathbf{r}' \otimes \mathbf{r}' \right) \right] \end{aligned}\]Let’s now simplify the terms.
By definition, \(\int \mathbf{r}' \, dm = 0\). Cross terms involving \(\mathbf{r}_{\text{cm}} \cdot \mathbf{r}'\) or \(\mathbf{r}_{\text{cm}} \otimes \mathbf{r}'\) vanish.
Splitting into CM-relative and CM-independent terms: \(\mathbf{I} = \underbrace{M \left[ r_{\text{cm}}^2 \mathbf{1} - \mathbf{r}_{\text{cm}} \otimes \mathbf{r}_{\text{cm}} \right]}_{\text{Term 1}} + \underbrace{\int dm \, \left[ r'^2 \mathbf{1} - \mathbf{r}' \otimes \mathbf{r}' \right]}_{\mathbf{I}'}\)
Term 1 is the inertia due to translating the axis to the CM. \(\mathbf{I}'\) is the inertia tensor about the CM.
Combining these results we obtain:
\[\boxed{ \mathbf{I} = \mathbf{I}' + M \left[ r_{\text{cm}}^2 \mathbf{1} - \mathbf{r}_{\text{cm}} \otimes \mathbf{r}_{\text{cm}} \right] }\]which is the generalized parallel axis theorem, also known as the Huygens-Steiner theorem.
